Complex Imperfect Objects
ereg is a molecular mechanics program. On an abstract level, the program consists of 2 objects: an energy function defined over the space of conformations available to the mechanical system and an algorithm for searching subspaces of the space of conformations in an attempt to minimize globally the energy function. Success in structure prediction requires of the energy function accuracy, enough that the global minimum occurs at the native structure, and of the search algorithm efficiency, enough that the multiple minima problem on the energy surface can be overcome in reasonable time. A concept central to the development of the program has been selective pressure on the 2 component objects created by the application of structure prediction. When the efficiency of the search algorithm is adequate, structure prediction selects for changes to the energy function that increase accuracy. Conversely, when the accuracy of the energy function is adequate, structure prediction selects for changes to the search algorithm that increase efficiency. Without a much larger input of resources, neither object could have advanced to its present utility, had the work focused on that object in isolation.
The Energy Function Object
The ereg energy function ( Fr +Fe +Fs +Ft +Fb +Fc +Fh +Fm +Fg +Fp) is a sum of components. Energy is defined over the space of conformations for a mechanical system constrained to rigid geometry.
Components Fr, Fe, and Ft 2,3,4
Accepting the anisotropic nature of atomic charge densities, the electrostatic component Fe is represented using a monopole, dipole, quadrupole, octopole, and hexadecapole positioned at each nucleus. The multipole expansion formalism is used to calculate interaction energies between pairs of anisotropic atomic charge densities. Relative to more standard representations based on the approximation of isotropic atomic charge densities, this representation enables greater accuracy without too much added computation. Relative to repulsion or dispersion interactions between atom pairs, electrostatic interactions decrease more slowly with distance. No cutoff distance, beyond which interactions are ignored, is used. Of greater impact to structure prediction, the machinery introduced here for calculation of Fe between pairs of anisotropic atomic charge densities is critically reused in representation of interaction energies between H-bond donors and acceptors. Although attributed to flow of electron density and accumulated to Fp, these (donor,acceptor) atom pair interactions are strongly anisotropic, driving the linearity of H-bonds.
The form of the repulsion +dispersion component Fr reproduces, at small interatomic distances, the softness seen in quantum mechanical data. Optimization of parameters of Fr includes fits to crystal structures and sublimation energies of 14 organic crystals.
Figure 1
H-bond Donor Fr Anisotropy
For Hydrogen bonding atom pairs, the functional form used to represent the Fr interaction energy was generalized from isotropic to anisotropic. Consider, for example, the peptide–peptide Hydrogen bond, and let θ be the N–H···O angle that describes the linearity of this interaction. The following notation is used for atom types: H02 for Hydrogen bonded to Nitrogen, O13 for carbonyl Oxygen, and H00 for aliphatic Hydrogen. Using Fr(H02,O13) to denote the unmodified, isotropic form of the repulsion +dispersion pair potential, we substitute the modified, anisotropic form Fr_aniso(H02,O13)= Fr(H02,O13)cos(θ)4 +Fr(H00,O13)(1-cos(θ)4). This substitution introduces independent control of the Fr pair potential along, and perpendicular to, the H–N axis. The effect is a large, soft Hydrogen perpendicular to the H–N axis, and a Hydrogen bond donor Hydrogen parallel to the H–N axis.
Component Fb
For the 5-atom rings of proline, ribose, and deoxyribose, torsion angle degrees of freedom are not constrained to regularized values by rigid geometry. Also not rigidly constrained are 1 bond length and 2 bond angles formed as a rigid-geometry side chain branch of the mechanical system crosslinks to the rigid-geometry main chain to model covalent closure of the ring. A sum of harmonic distance constraints functional form is used to represent energies of covalent bond stretching, bond angle bending, and planar distortion attributed to imperfect closure of the 5-atom rings.
Components Fh and Fm 4
Hydration free energy is formed as the combined energy of two distinct models. Hydrophobic energy Fh is the energy of a hydration shell model. The calculation of Fh substitutes a gaussian volume estimate for hydration shell volume. The remainder of hydration free energy Fm is the interaction energy of the mechanical system with a continuous dielectric medium. The calculation of Fm uses a boundary element solution to the Poisson equation, an order n3 computation, where n is the number of boundary elements of a molecular surface. Relative to evaluation of Fe, evaluation of Fm is an order of magnitude more expensive. Although code has been created for calculating analytical 1st and 2nd derivatives of the Fm component, the calculation is too slow to support useful movement on the full energy surface. As a consequence, trajectories of the 3 types used in the search algorithm object (local minimization, ascent, and inflation) are carried out on an approximation to the full energy surface in which the Fm component is replaced by Fw. Search algorithms attempting global energy minimization on the full energy surface include the dielectric medium component Fm as a single point function evaluation at the end points of local minimization trajectories.
Component Fp
Energy contributions attributed to electronic polarization are accumulated to Fp. Contributions to Fp, selected based on positive impact to structure prediction, partition into 4 types based on physical origin. Each type of contribution is represented by its own functional form.
Type 1 is flow of electron density in formation of H-bonds crosslinks. The functional form used is a multipole expansion between a dipole and quadrupole placed on both the donor and the acceptor. The result favors linear H-bonds that can be directed toward lone pairs. This type of interaction between a (donor,acceptor) atom pair differs from an Fe component interaction between a pair of anisotropic atomic charge densities in that no interactions are calculated between (donor,donor) or (acceptor,acceptor) pairs.
Type 2 is polarization of electron density in formation of networks of H-bond crosslinks. Here, electronic polarization can either reinforce, as occurs in α-helices and β-sheets where aligned peptide planes form chains of H-bonds, or interfere, as occurs in bifurcated H-bonds. The functional form used is a product of 2 type 1 functional forms multiplied by a constant coefficient. The coefficient is positive or negative, depending on whether the chained pair of H-bonds interfere or reinforce, respectively. This type of contribution is evaluated for all chained pairs of H-bonds.
Type 3 is modulation of peptide dipoles based on secondary structure or, alternatively, with the relative orientation of peptide planes adjacent along the sequence. The functional form used is the type 1 functional form multiplied by a factor dependent on the backbone conformations of the 2 residues linked by the peptide plane. The result is a slight stabilization of β-sheets and a slight destabilization α-helices.
Type 4 is the lower polarizability of nonpolar functional groups in comparison to polar functional groups in the electric field of ionized groups. The functional form used is gaussian 3-body volume. The result is a destabilization of nonpolar atoms in locations where the electric field created by the ionized groups is strong.
Component Fg
In the following description, we use the n-m notation for characterization of peptide–peptide H-bonds, where n is the number of residues separating the donor H and the acceptor O, and m is the number of atoms in the cycle completed by formation of the H-bond. Attributed to chain entropy, component Fg, is represented as a step function defined over patterns of peptide–peptide H-bond crosslinks. More specifically, the following patterns of peptide–peptide H-bond crosslinks, with some exceptions for occurrences of Glycine, are associated with reduced chain entropy: 1) H-bonds outside of a helix or sheet, 2) multiple H-bonds to a single donor or acceptor, 3) 3-10 and 5-16 H-bonds to a bifurcated acceptor, 4) consecutive 5-16 H-bonds, 5) 4-13, 5-16 H-bonds to consecutive acceptors.
A Careful Treatment of Electrostatic Energy
Each component of electrostatic energy, here defined broadly as (Fe +Fh +Fm +Fp), the sum of energy components for which the branch of physics theory most useful for a description is classical electorstatics (including polarization), is represented using a detailed, non-standard functional form. For each component of electrostatic origin, the application of structure prediction has selected for modifications moving toward more detailed representations. Consistently, the Fe component uses no cutoff distance, beyond which interactions are neglected.
Approximate Energy Surface
Trajectories of the 3 types used in the search algorithm object (local minimization, ascent, and inflation) are generated on the (Fr+Fe+Fs+Ft+Fb+Fc+Fh+Fw+Fp) energy surface, with charges on ionized groups scaled to 9/64 of full values. This approximation to the full (Fr+Fe+Fs+Ft+Fb+Fc+Fh+Fm+Fg+Fp) energy surface excludes Fg and replaces Fm with Fw, the energy of a simple hydration shell model for which calculation of analytic 1st and 2nd derivatives is more tractable. To support local or global energy minimization on the full energy surface, full energies are calculated, using charges on ionized groups restored to full values, as single point function evaluations at the endpoints of some local minimization trajectories.
The Search Algorithm Object
The ereg program uses rigid-geometry molecular mechanics, meaning bond lengths, bond angles, and some torsion angles are held fixed. The rigid geometry constraint, by reducing the number of degrees of freedom, supports calculation of analytical second derivatives. Availability of second derivatives contributes to the efficiency of search algorithms by enabling powerful methods for calculation of steps on the approximate energy surface. Joined in sequence, steps calculated to accomplish the same purpose, either local minimization or ascent, form a trajectory on the approximate energy surface. Trajectories on the approximate energy surface are used as building blocks in construction of the ereg search algorithms.
Segment Deformation Search 1
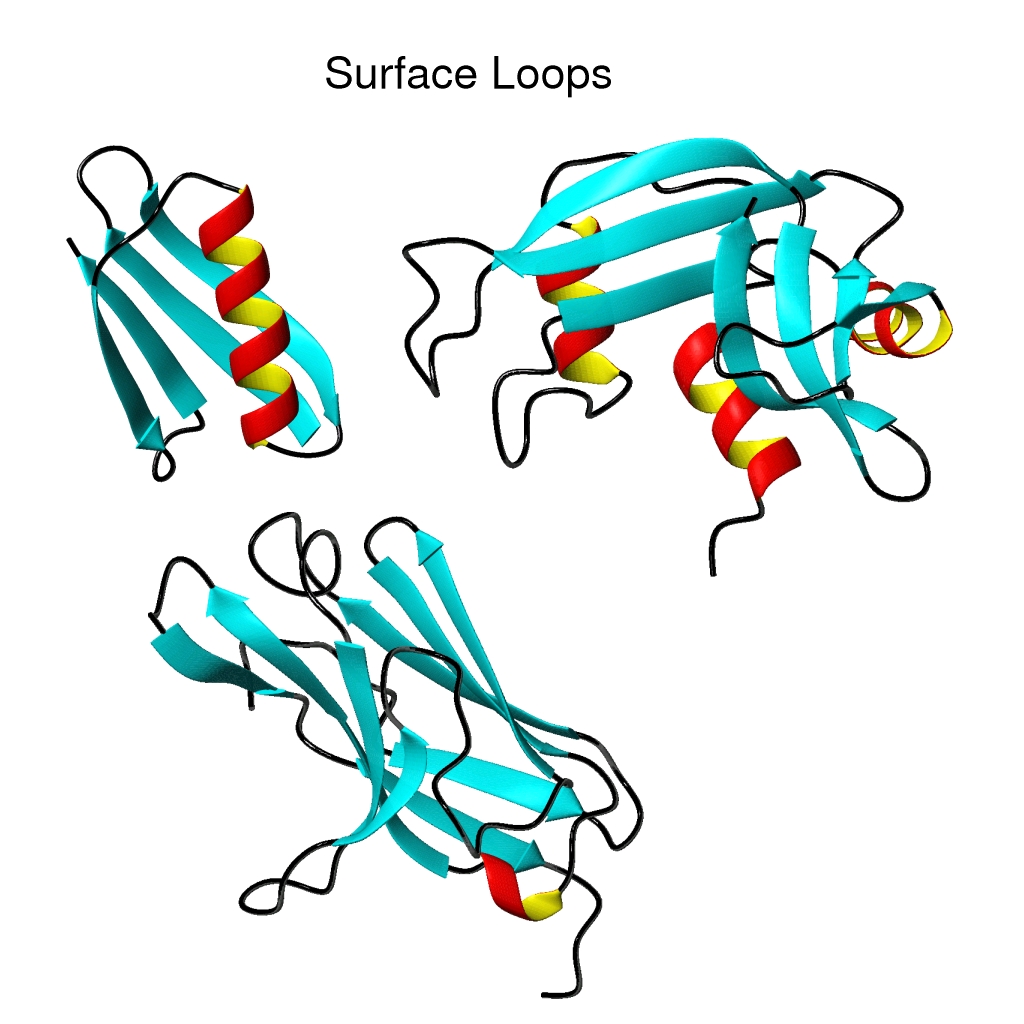
Using as starting points a collection of segment deformations, the algorithm generates local minimization trajectories on the approximate energy surface. Single point evaluations of full energy at the endpoints of the local minimization trajectories produces a collection of low-energy local minima on the full energy surface. This search algorithm is able to overcome the multiple minima problem for the specific case of protein surface loops in the presence of a fixed core.
The following concepts contribute to efficiency. The algorithm generates backbone deformations for the segment, distributed uniformly over the space of backbone deformations, and excludes, using a screen score function, deformations unlikely to be productive. The algorithm removes overlaps from starting conformations, and excludes deformations from which overlaps cannot be removed. For each overlap-free backbone conformation, the algorithm generates a local minimization trajectory with respect to a subset of degrees of freedom. This subset consists of backbone torsion angles of the deformable segment and side chain torsion angles for side chains that can contact the deformable segment but are not marked as searchable. Interactions involving side chains marked as searchable are excluded. Also, interactions between the N- and C-terminal rigid segments that border the deformable segment are excluded. Here, distance constraints are used to maintain fixed the relative position and orientation of the adjacent rigid segments. For each low-energy backbone conformation, the algorithm generates a low-energy side chain conformation using dead-end elimination search through the combinatorial space of side chain rotamer conformations. This lattice search is followed by off-lattice overlap removal and generation of local minimization trajectories with respect to variable side chain torsions.
Multiple Segment Deformation Combinatorial Search
The number of local minima produced by deforming a 7-residue surface segment is typically on the order of 2–8 thousand. The segment deformation search algorithm was extended to enable multiple segment deformations. The complete chain of a small protein, or a region of the complete chain of a larger protein, is partitioned into multiple segments of length 7-13 residues. Backbone deformations are generated for each of the segments. In a procedure analogous to the commonly used procedure for combinatorial search of side chain rotamer conformations, the backbone segment deformations are fed into a combinatorial search using dead-end elimination to select the collection of 2–4 thousand combinations of deformations having lowest energy. These optimal combined deformations are used as starting points for generation of local minimization trajectories on the approximate energy surface with respect to backbone torsion angles. From this point, the search algorithm continues unchanged from the algorithm used for a single segment deformation.
The above algorithm has been adapted for parallel execution on multiple processors. The chain can be partitioned into multiple alternative sequences of deformable segments. For each partition, the search through the combinatorial space of deformations can be distributed to its own processor.
Igor Model Fold Prediction 8
For each residue of a single polypeptide chain, the continuous space of conformations is replaced by 3 states {H,E,C}, abbreviations for the elements of secondary structure {helix, extended, coil} to which the residue can contribute. The set of chain states is the set of mappings from the set of residues into {H,E,C}. Letting n be the number of residues, the number of chain states is 3n. The set of element compositions is the set of mappings from the set of pairs of consecutive residues into a binary decision: either extension of the current string or transition between strings. The number of element compositions is 2(n-1). For each chain state and pair of consecutive residues, association of states {HH,EE,CC} with extension of the current string, and states {HE,HC,EH,EC,CH,CE} with transition between strings, defines a mapping from the set of chain states to the set of element compositions.
For a single polypeptide chain, the igor model consists of the replacement of the continuous space of conformations with a discrete set of chain states, and a score function defined over the set of element compositions. The igor model is a generalization of a residue Ising model. The residue Ising model is short range in the sense that residue i interacts directly only with neighboring residues in the range {i-5,...,i+5}. The igor model extends the residue Ising model to include residue-residue interactions of intermediate and long range.
A fold is a full-atom structure model generated for a sequence of helices, extended strands, and connecting coil segments by maximizing the long range component of the igor model score function over the space of packed configurations. The search through packing space, a part of the igor model search through the space of element compositions, is accomplished as a sequence of 2 conceptually similar searches: the packing of strands into sheet configurations, followed by the packing of helices and sheet configurations into folds. The packing algorithm produces both the long range component of the igor model score, which enables more meaningful scoring of the element composition, and a full-atom structure model, which can be used as a starting point for subsequent molecular mechanics-based structure prediction. A search through the space of element compositions of the low-resolution igor model generates a collection of high-scoring folds. In testing on domains having experimental structures, the native fold is often recovered in the collection of high-scoring folds. Assisted by the simple nature of the igor model, the search algorithm largely succeeds at recovering the element composition and fold that maximize globally the igor model score and long range component, respectively. Conversely, limited by the simple nature of the igor model, the score function and long range component only moderately succeed at assigning global maximum values to the native element composition and fold, respectively.
Guided Trajectory Search 9
Starting from a local minimum on the full energy surface, the fundamental unit of computation, referred to as a cycle, generates a neighboring local minimum on the full energy surface such that the targeted range for the RMSD from the starting local minimum is [2–4] Angstroms. Global minimization is attempted as a sequence of cycles from which a trajectory of local minima is assembled by using a Monte Carlo criterion to decide acceptance or rejection for each new local minimum. Each cycle generates a trajectory on the simplified approximation to the full energy surface. The cycle trajectory attempts to minimize globally on the approximate energy surface, meaning the cycle trajectory attempts to pass over barriers into regions of the space of conformations containing local minima having lower energies. At the endpoint of each cycle, full energy is obtained as a single point evaluation, and a Monte Carlo acceptance decision is made based of full energy.
A cycle trajectory is a composite formed by linking trajectories generated by 3 distinct algorithms: the algorithm used to generate a local minimization trajectory, and 2 variants of this algorithm. The first variant generates an ascent trajectory that climbs barriers and passes through saddle regions. Directions of ascent are prioritized based on gradients along these directions of a subset of energy components that is targeted for reduction in the current cycle. In contrast to a physical trajectory, meaning a solution to the equations of motion for a constrained mechanical system, an ascent trajectory represents an attempt to sense by analysis of the local energy surface which directions of ascent will be most productive toward a goal of entering regions of conformation space associated with lower energy local minima. The second variant generates an inflation trajectory that deforms the approximate energy surface such that motion favorable to the Fe, Fh, and Fp components is facilitated.
Let p be atomic radii for a subset of atom types. And let x be coordinates for a subset of torsion angle degrees of freedom. A trajectory through the combined space of parameters and torsion angles is generated by minimization of a target function K(p)=(Ky(x(p)) +Kw(p)) with respect to p. The torsion angles x also vary, but are dependent on p. The function x(p) is determined by the constraint that x(p) be a local minimum conformation on the approximate energy surface with respect to x. The approximate energy surface depends on p through the dependence of Fr(p,x), the repulsion +dispersion component, on atomic radii.
Components of the inflation target function have physical meaning as follows. Ky=( Fe +Fh +Fp). Kw drives inflation by decreasing in value as atomic radii expand. The combined effect of minimizing these target function components is expansion of atomic radii, pushed by decrease of Kw(p), on a path through parameter space that is biased toward minimizing ( Fe +Fh +Fp).
At the innermost level of nesting, the smallest repeatable unit of computation, referred to as a composite step of the cycle trajectory, is formed as 1) 128 steps of a local minimization trajectory, 2) 512 steps of an ascent trajectory, starting from the endpoint of the local minimization trajectory, and 3) 1 step of an inflation trajectory starting from the endpoint of the ascent trajectory. Each cycle trajectory consists of 1) an adaptable number of composite steps, 2) restoration of the original (physically meaningful) atomic radii, and 3) 128 steps of a local minimization trajectory. The number of composite steps adapts to maintain the RMSD between neighboring local minima produced in consecutive cycles in a targeted range of [2–4] Angstroms.
As a tool for search of conformation space, guided trajectory search complements segment deformation search. The segment deformation search, by focusing computation on a spatially localized region of a larger structure, is more efficient when changes to conformation are concentrated within 1, or more, segments. Also, generation of deformations distributed uniformly, by not considering energetic barriers between deformed and undeformed conformations, provides a mechanism for catalyzing some topological chain transitions for which large transition state energies might slow progression of a trajectory search. The guided trajectory search, by enabling full chain flexibility, facilitates large, distributed motions such as changes to the packing configuration for a collection of helices and sheets.
Selective Pressure
Protein Surface Loops
Figure 2
Following creation of the segment deformation search algorithm, segments of protein crystal structures, allowed to vary in conformation and interacting with the external field of the rest of the structure, provided systems for which the native structure, assumed equal to the crystal structure, was known, and for which global minimization on the energy surface was possible. Applications of segment deformation search to surface loops of protein crystal structures consistently produced structures that differed from the crystal structure yet had lower energy, suggesting errors in the initial energy function. We note that protein structure prediction is an exceptionally demanding application. In an attempt to reduce errors in predicted structures, parameters and functional forms were altered. The theory of molecular forces provides a framework for constructing variants to the energy function. The energy of a system of molecules can be usefully resolved into the following components.
- repulsion
- dispersion
- electrostatic
- polarization
- bond stretching
- bond angle bending
- intrinsic torsional
- hydration free energy
Changes to these components led to successful prediction of structures of protein surface loops. Other results significant to the ereg meta project included: code for calculating distributed atomic multipoles from wavefunctions, code for implementing a multipole expansion representation of electrostatic energy, and code for calculating the energetic effects of a dielectric continuum based on a boundary element solution to the Poisson equation.
Small Proteins
For small proteins, although global minimization on the energy surface remains a challenge, applications of the guided trajectory search algorithm starting from folds produced by the igor model supports assembly of data sets of low-energy decoy structures. Small proteins not containing disulfide bond crosslinks provided systems for which some decoy structures differed from the native structure, assumed equal to the experimental structure, yet had lower energy, suggesting errors in the energy function. Analysis of data sets of incorrectly predicted structures led to addition of proline ring flexibility, to addition of new components Fp and Fg, and to continued improvement of Fm. Incorporating these changes, the current energy function less commonly produces decoy structures having lower energy relative to the native structure.
Molecular Mechanics Functionality
Protein Design 7
The initial functionality of the program was molecular mechanics-based prediction of protein structure. Over a period of several years, the energy functions and the conformational search algorithms evolved under the selective pressure of success in this initial application. Sequence design functionality was obtained from the initial structure prediction functionality by addition of reference states –for example the unfolded state for design of thermodynamic stability, the unbound conformation for design of binding affinity, or the amorphous solid state for design of solubility– along with search through residue sequence space. For each sequence of a specified space of sequences, the program searches through a specified space of conformations. The lowest-energy conformation found is used to evaluate dG, an estimate of free energy of folding. Because different models are used to represent the folded state of the protein and the reference unfolded state, dG is not, for a single sequence, a physically meaningful measure of stability. However, ddG=( dG(sequence1) -dG(sequence0)), the change in dG with sequence, does provide a meaningful measure of relative stability. The free energy of the unfolded state is estimated as the free energy of an Ising model representation.
pKa of Ionizable Groups 7
The same methods added to ereg to enable sequence design also enable prediction of pKa for ionizable residues. A common use of this functionality is to calculate the most probable ionization state for a specified pH, and to generate a most probable conformation consistent with this ionization state. This usage enables subsequent modeling of the most probable sequence, including protonation state, for a given pH. Also enabled by this functionality are calculations of pH dependence of protein stability and solubility.
Nucleic Acids
By introducing a generalization of the concept of residue, much of the protein functionality of ereg has been extended to oligonucleotides. For nucleic acid chains, the most natural choice for the monomer unit of composition, the nucleotide, was not used. Instead, each nucleotide is partitioned into an ordered triple of residues (a pentose ring, a nucleic acid base, a backbone phosphate). This choice, although it imposes a burden of required preprocessing for structures taken from the PDB database, was considered preferable to a combinatorial explosion of residue types. In addition to the ribose and deoxyribose sugars and to the phosphodiester linkage that make up natural DNA and RNA, the residue data set includes some of the more common chemical modifications of these building blocks, for example the phosphorothioate linkage.